Petri nets
Chapter 1: What?
Where we learn what a Petri net is.

This is a place.

A place can hold tokens (here 3).

This is a transition.
A transition can never hold tokens, no no.

This is an arc.

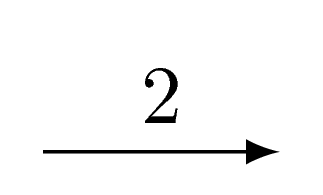
An arc may be decorated with an integer (whose value is at least 1).
Putting no such number means it is 1.

An arc can link a place to a transition, or the other way round.

But an arc cannot link two places nor two transitions. Never, never.

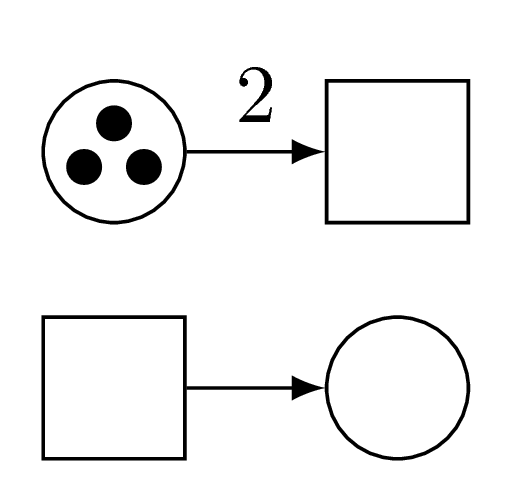
This is a Petri net, let’s call it Carl.
Carl has one transition, two places (one with three tokens, the other with none), and two arcs.

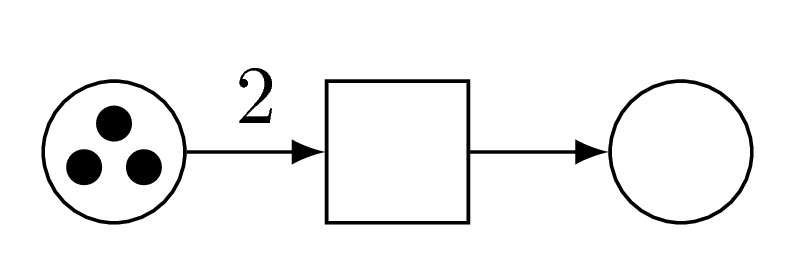
Transitions consume and produce tokens in places, according to what arcs indicate.
Carl’s transitions can consume two tokens in the leftmost place, and produce one in the rightmost place.
(1 is not indicated because hey, it is 1.)
If it does, we say that the transition has fired.

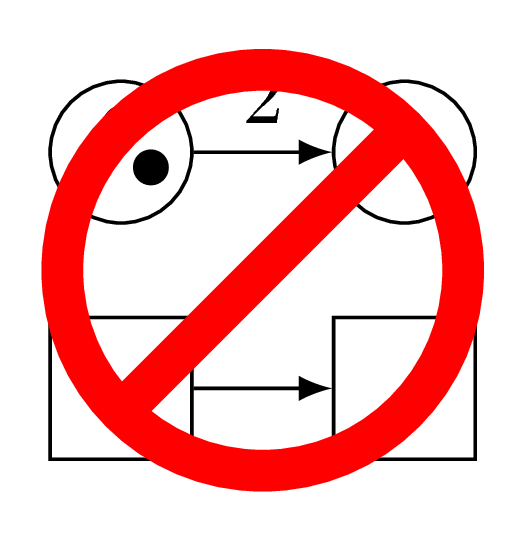
Here, Carl has fired its transition.
Two tokens have disappeared from the leftmost place, and one has been added to the rightmost place.
As indicated by the arcs.

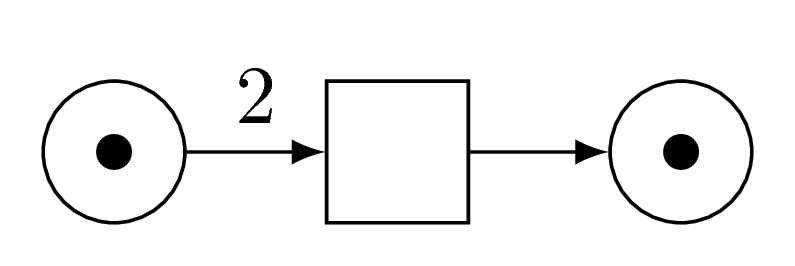
Now, Carl cannot fire its transition anymore, because it cannot consume two tokens in the leftmost place.
So Carl is blocked.
(Poor Carl.)

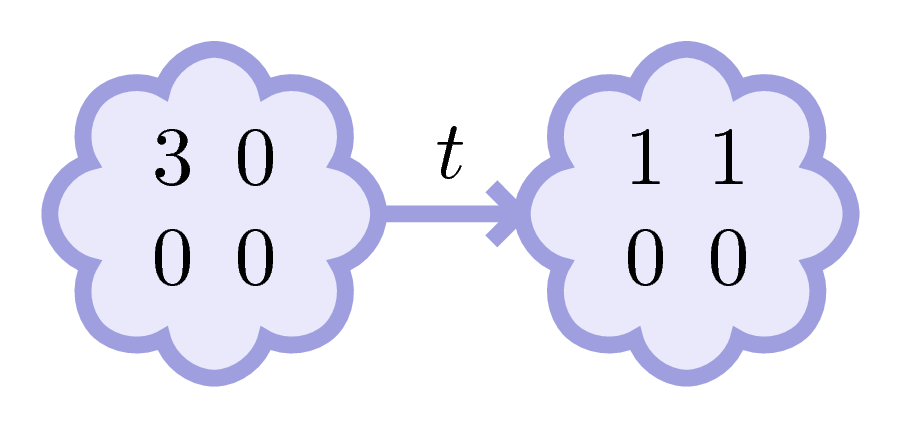
This is another Petri net, let’s call it Adam.
Since it has many places and transitions, we give them names: \(a\), \(b\), \(c\), \(d\) for the places, and \(t\), \(u\), \(v\), \(w\) for the transitions.

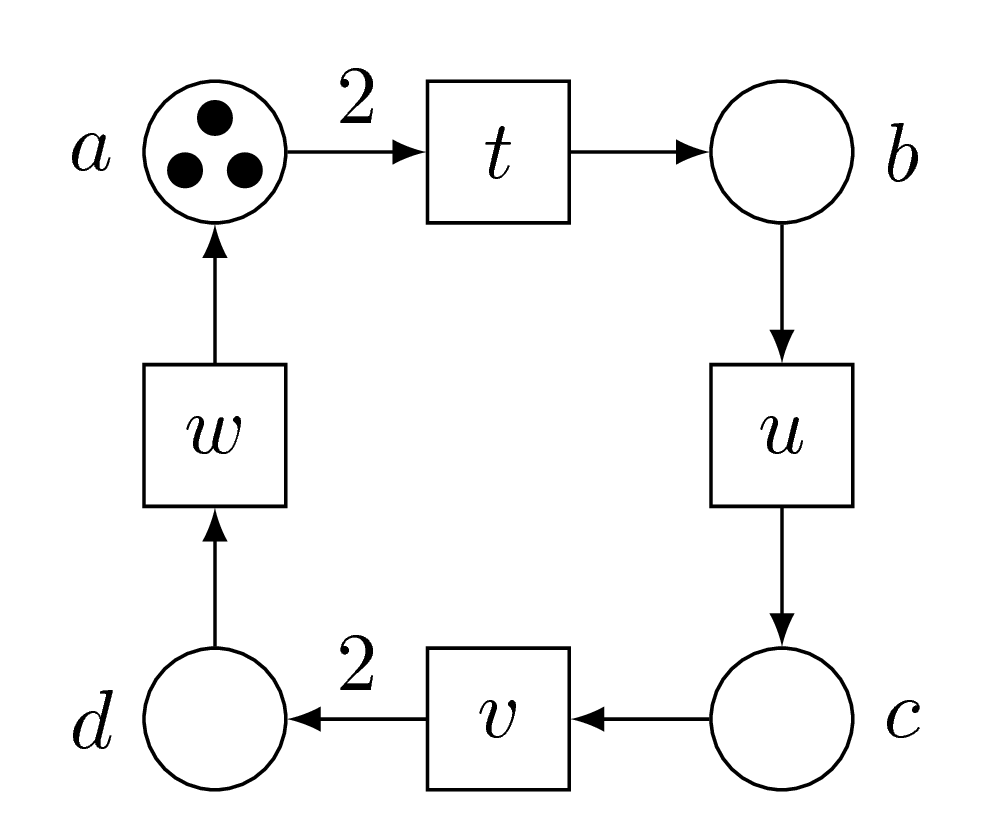
Adam has 3 tokens in its place \(a\), and no tokens elsewhere.
We call this its marking, that is, the number of tokens in each place.
We may draw it as a little blue cloud.

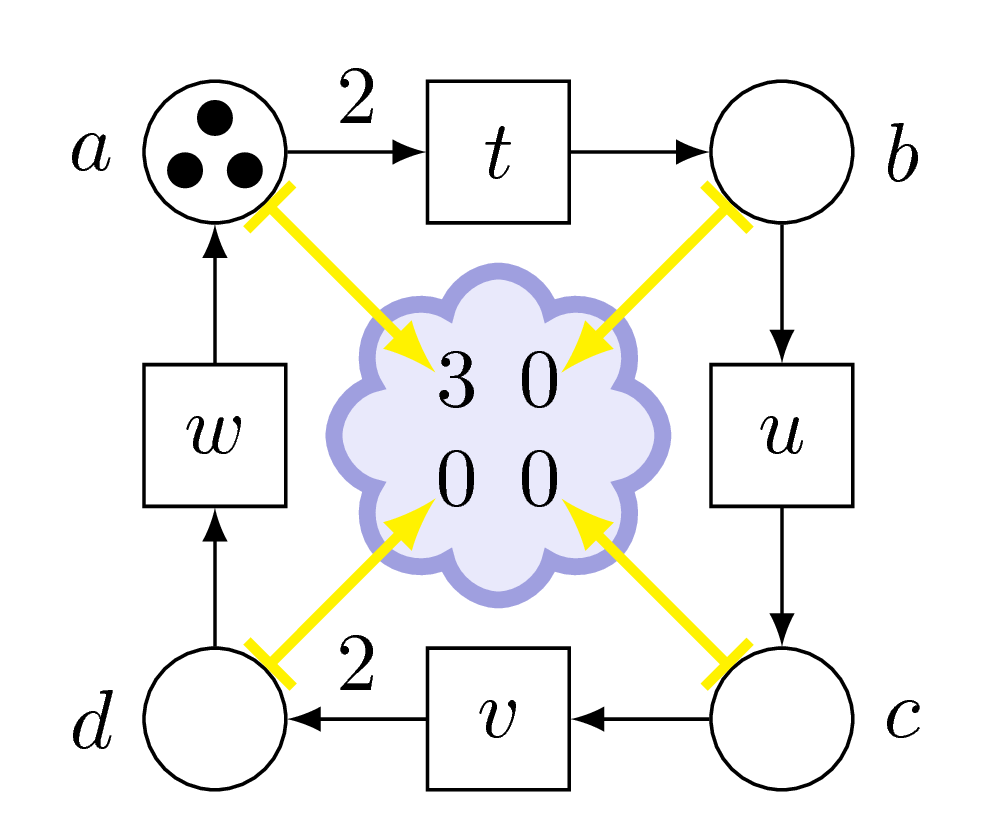
Adam can fire its transition \(t\), we will remove two tokens from \(a\), and add one to \(b\).
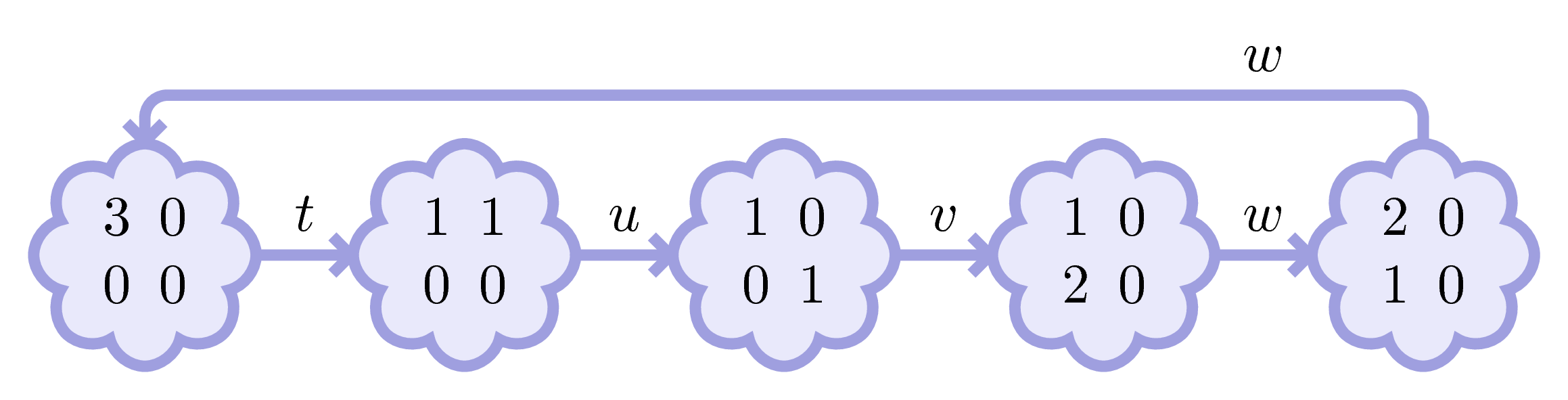
This yields this marking.

We may represent this evolution from one marking to another as a graph.

And this graph may be extended by firing \(u\), \(v\), and \(w\).

From the last reached marking, we can fire \(w\) again, and we go back to the initial marking.

But wait! Not that fast… Instead of firing \(w\), we could have fired \(t\) because there was two tokens in \(a\).
Consequently, we obtain a branching in our graph.

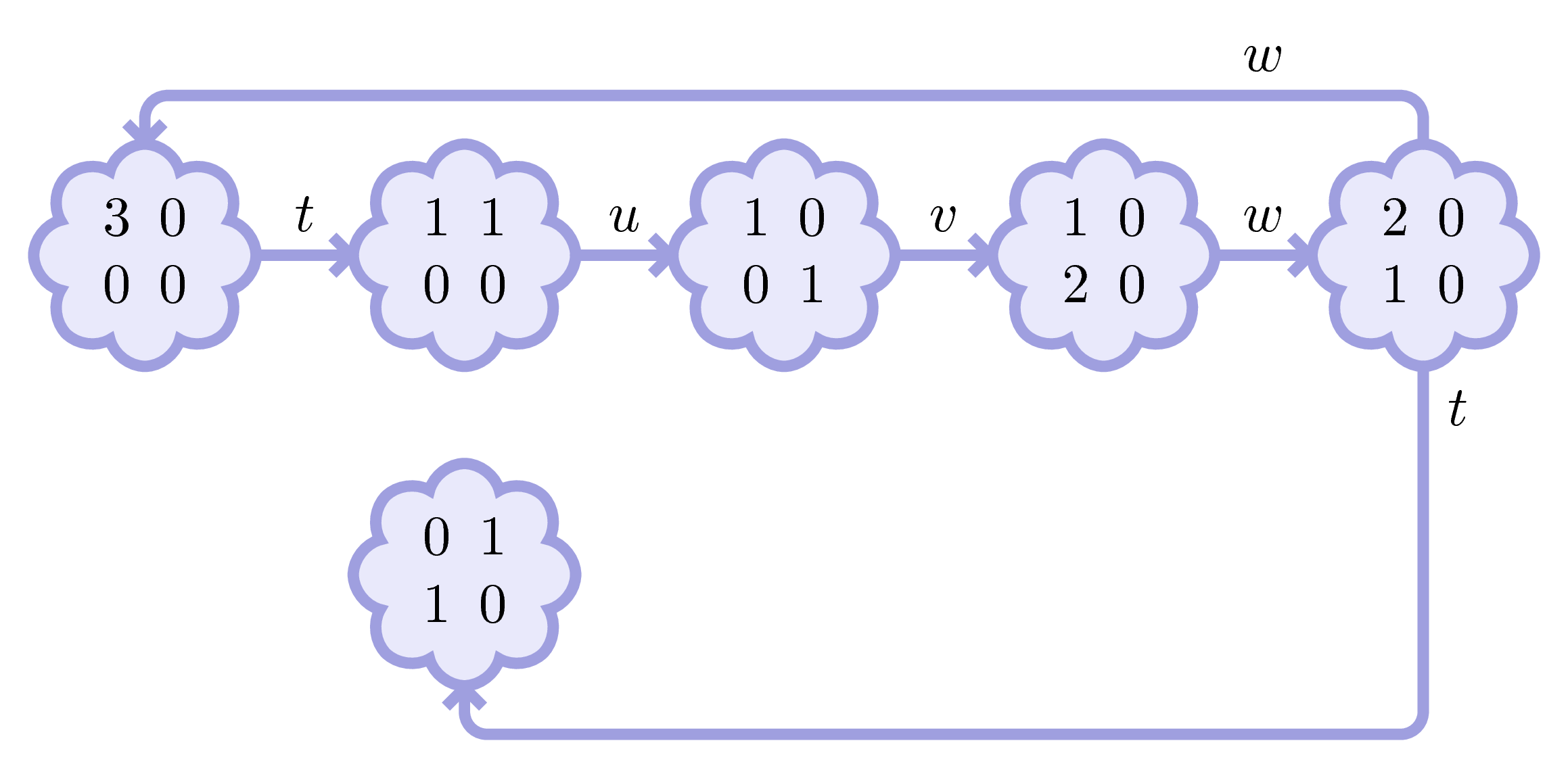
We continue: from every marking, we fire every possible transition.
And we obtain what we call the marking graph.

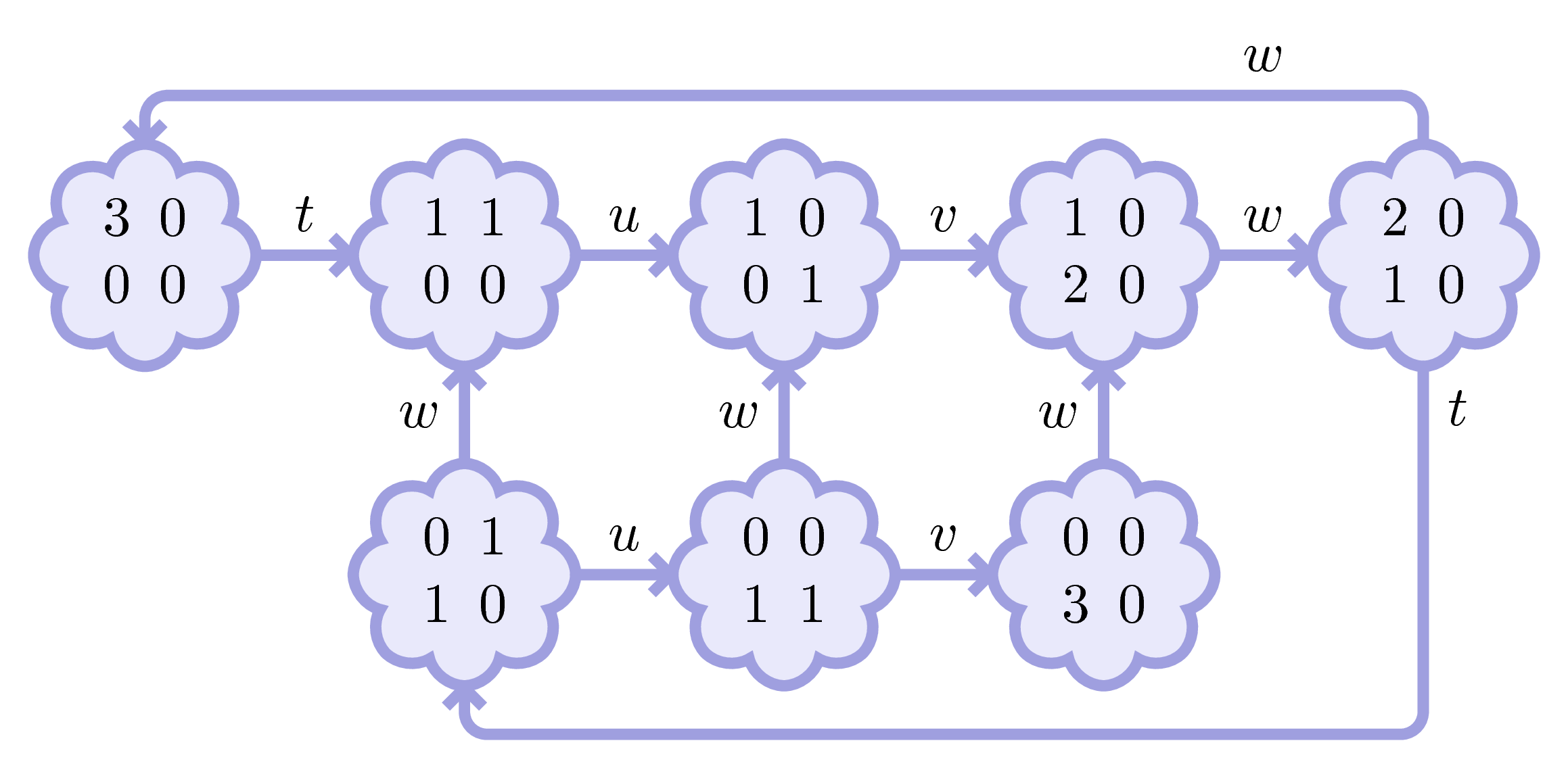
Let’s replay this action in slow motion… We note that Adam, contrarily to Carl, has no blockages.
(It’s a fulfilled net.)

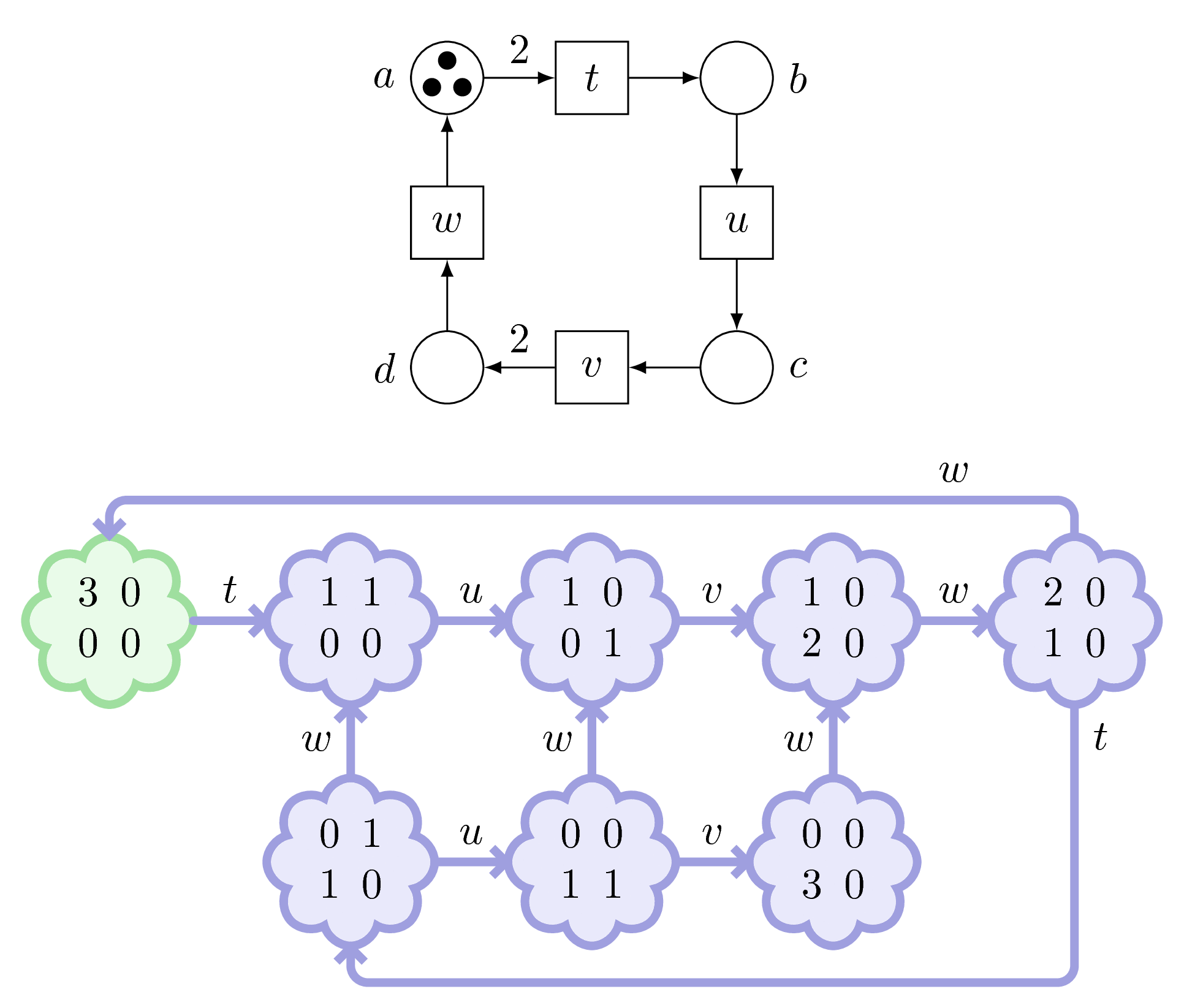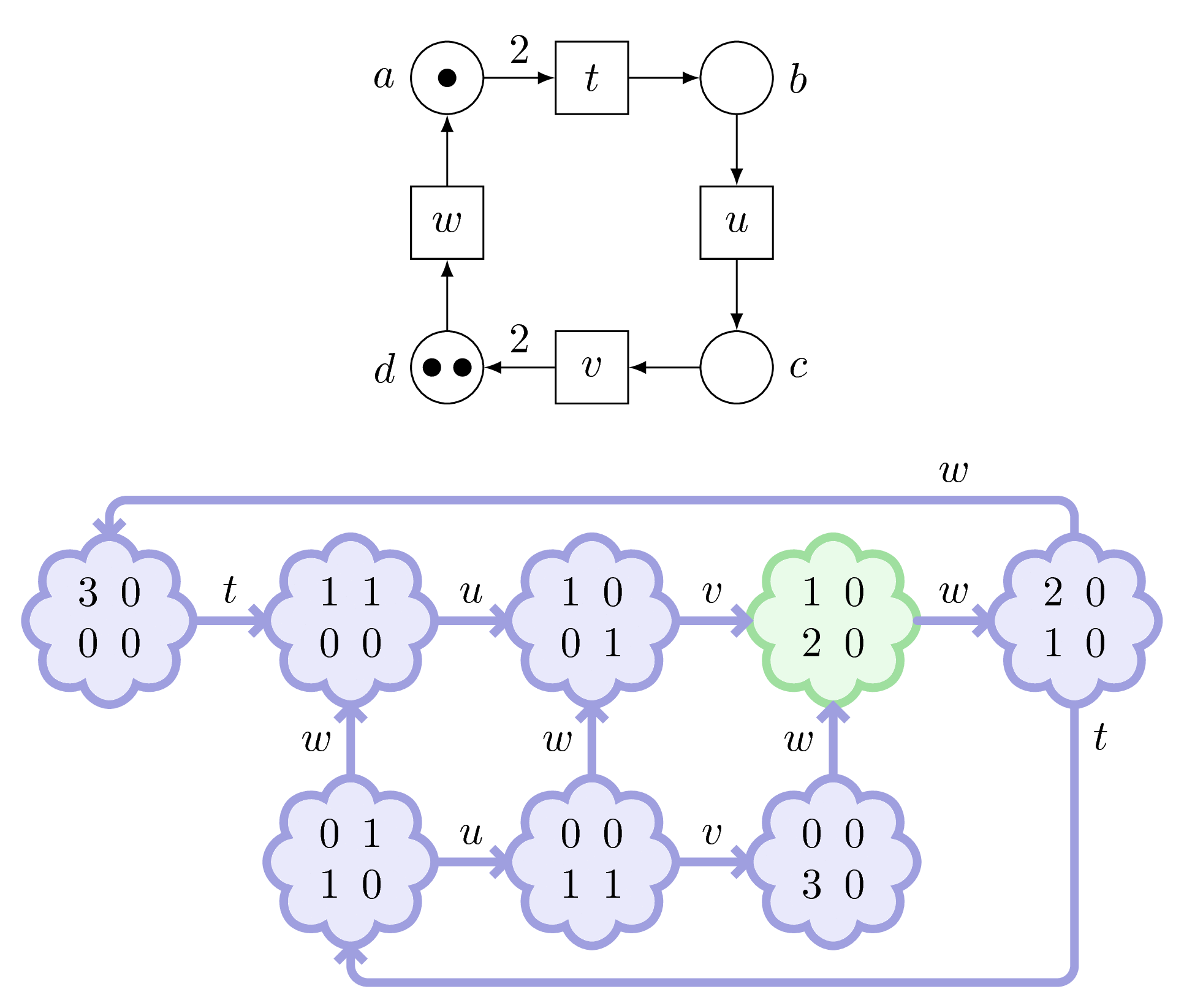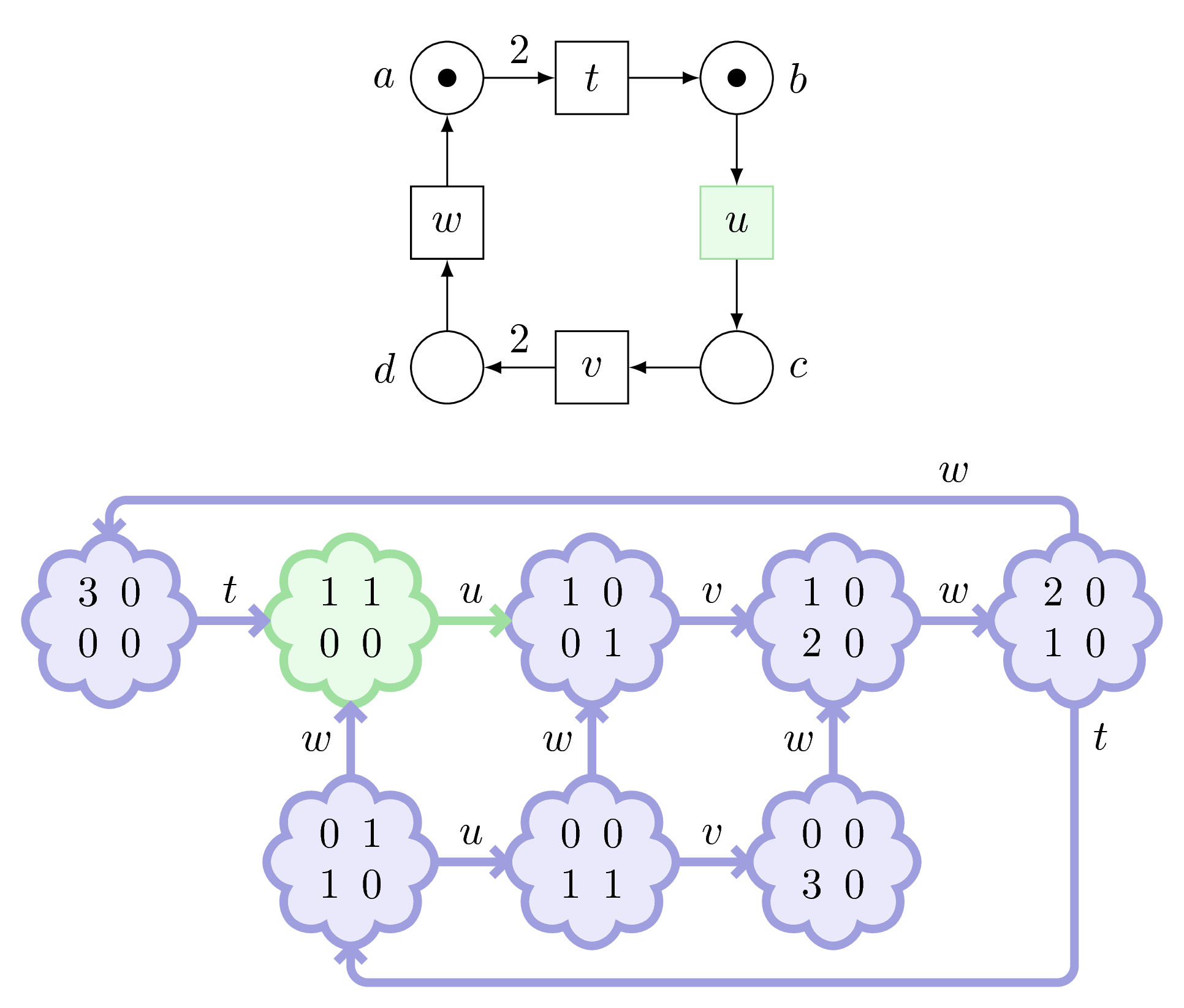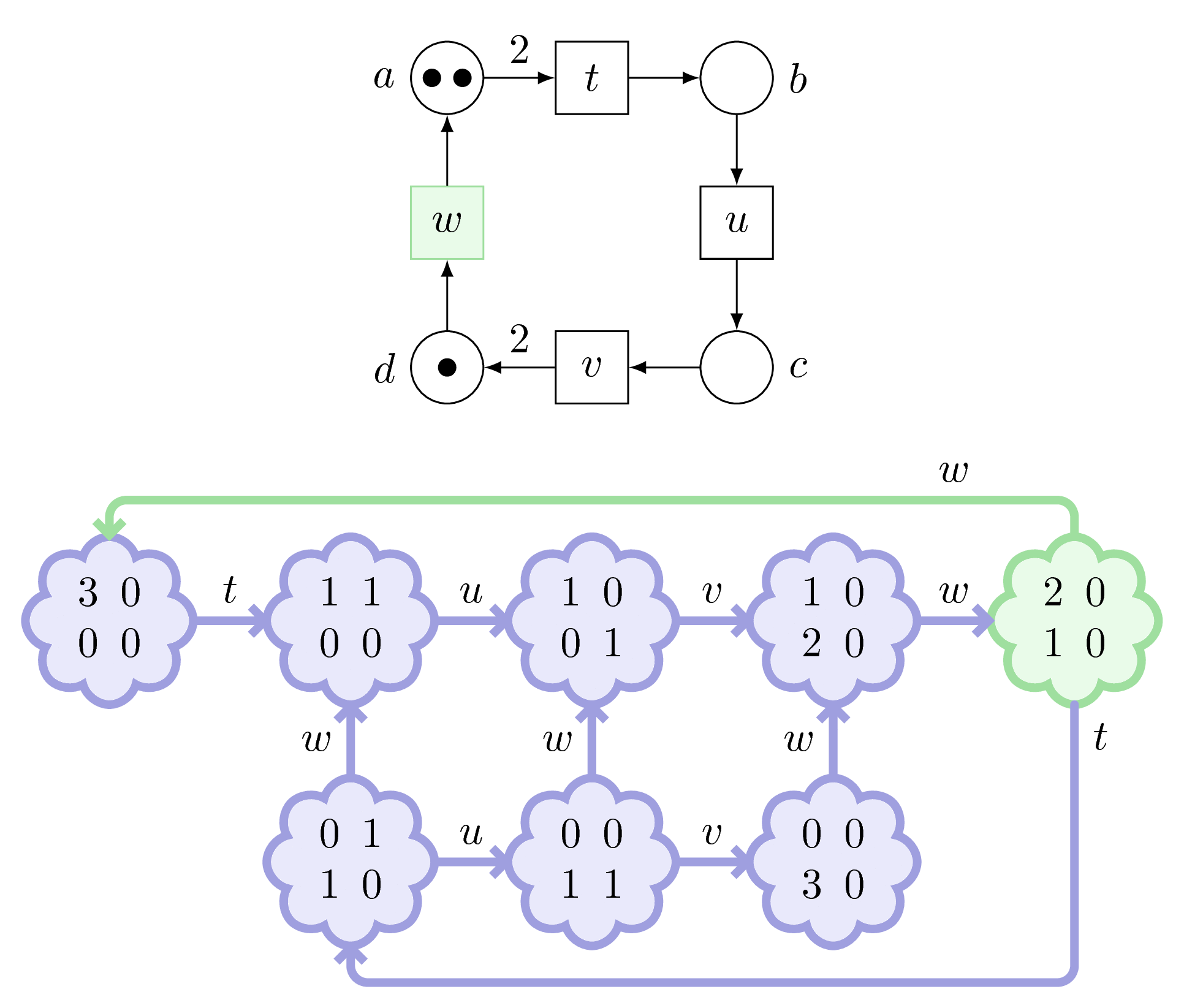
Our Chapter 1 is now terminated.
See you soon for Chapter 2: Why?